Real Case

Real Case adalah bentuk pemetaan yang di bagi menjadi industri dan tempat lainnya atau dari kepadatan penduduk atau bangunan yamg kita metakan.,

kemudian Tujuan GIS di bidang Industri adalah :

1. Pemetaan kawasan yang sesuai untuk keperluan pembuatan pabrik
2. Pemetaan jalur distribusi produk.

begitupun industri memiliki menset yaitu :

-Setiap barang punya lokasi tempat yang ditetapkan dan barang tersebut selalu diatur kembali ketempatnya pada waktu yang ditetapkan pula.
-Setiap proses punya syarat ketrampilan apa yang dibutuhkan dari operatornya, jelas batas baik buruknya, jelas urutan kerja dan ukurannya, jelas alat dan bahannya, jelas cara kerjanya, jelas kondisi kerjanya, jelas apa yang boleh dan tidak boleh dilakukan, dst.
-Setiap material yang digunakan punya tuntutan spesifikasi yang jelas dan dipastikan bukti pemenuhannya dengan sampling pengujian berkala dsb.
-Setiap lokasi dan aset ada penanggung jawabnya dengan aturan kebersihan, keteraturan, pemeliharaan yang jelas.

Bagaimana bisa, kita menciptakan diri kita yang sesuai dengan standart itu ?

• Mencari standart yang ada di tempat kerja yang kita inginkan, lalu bisa menguasai yang dibutuhkan
• Mencari tempat yang bisa memberikan kompetisi 
• Mencari orang yang ahli, ~> kurang inovasi dan kreatifitas, 

Cara memulai belajar mandiri yaitu dengan :

1. Pilih permasalahan yang diminati
2. Buat solusi singkat dan cepat, tidak perlu sempurna
3. Kembangkan dan perbaiki solusi tersebut
4. Tulis dan share solusi yang sudah dibuat
5. Ulangi langkah 1-4 untuk problem yang lain
6. Mengikuti komunitas/forum atau kompetisi secara serius
7. Terapkan metode2 dalam pekerjaan 
8. Mengajarkannya.

dengan contoh kita buat programnya menggunakan D3js dan WebGL

ini adalah bentuk di mana gambar2 tersebut mempunyai warna yang berbeda2 apabila tanda tersebut lebih panjang maka area tersebut telah banyak di kunjungi oleh UFO 

Demikian Penjelasan dari Real Case

Cost Distance Analysis

jarak biaya adalah "gagasan keluarga metrik jarak alternatif" . Ada banyak cara untuk mengukur jarak antara dua titik yang relevan dengan GIS, termasuk Euclidean distance (garis lurus yang tidak dibatasi),  Geodesic distance (ketika perjalanan dibatasi ke permukaan bola), dan  network distance  (saat perjalanan dibatasi ke jaringan linear). Jarak biaya menggunakan prinsip geografis Gesekan Jarak, yang menyatakan bahwa ada biaya atau impedansi yang terkait dengan pemindahan jarak unit ke lokasi mana pun, dan biaya ini bervariasi untuk ruang (dan dengan demikian dapat dikonseptualisasikan sebagai bidang). Misalnya, jika biaya seseorang yang melakukan perjalanan di ruang mana pun diukur ketika jumlah energi yang dikeluarkan, maka bergerak di atas air (mis., Berenang) memiliki biaya yang jauh lebih besar daripada bergerak di atas tanah (mis. Berjalan). Jika seseorang ingin meminimalkan biaya pengeluaran energi ini, maka mungkin lebih baik berjalan di sekitar badan air daripada berenang langsung melewatinya, meskipun jarak sebenarnya lebih besar. Biaya ini dapat diukur dengan berbagai cara. Meskipun pengeluaran finansial aktual dapat menjadi bagian darinya, gagasan "biaya" biasanya digunakan untuk setiap dampak negatif pindah ruang. Bergantung pada aplikasi tertentu, ini dapat mencakup:

•  Waktu perjalanan
•  Pengeluaran energi untuk perjalanan (misal : Penggunaan bahan bakar kendaraan)
•  Biaya perolehan properti
•  Biaya konstruksi
• Dampak negatif terhadap lingkungan alam (mis., Melintasi lahan basah atau membuka hutan)
• Dampak negatif terhadap lingkungan manusia (mis., Menghancurkan rumah atau bangunan bersejarah)

               Secara konseptual, seseorang dapat "mengukur" biaya jalur yang melintasi area unit ruang mana pun. Sebagai contoh, jika seseorang merencanakan jalur bersepeda beraspal, lokasi pada lereng berhutan curam kemungkinan akan berarti biaya konstruksi yang tinggi, dampak negatif yang tinggi terhadap lingkungan alam, dan biaya energi yang lebih tinggi untuk pengendara yang mencoba bersepeda di lereng. Atau, tanah kosong di lingkungan pinggiran kota yang datar akan memiliki biaya rendah dalam tiga hal ini, tetapi tanah mungkin lebih mahal untuk dibeli. Karena biaya yang berbeda ini menggunakan unit ukuran yang berbeda atau tidak dapat diukur secara langsung dengan cara kuantitatif apa pun, model Indeks sering digunakan untuk membangun "ukuran semu" dari total biaya untuk digunakan dalam GIS.

Seperti banyak bidang lainnya, biaya biasanya direpresentasikan dalam GIS menggunakan kisi-kisi raster yang dikenal sebagai permukaan Biaya, di mana nilai setiap sel mewakili total biaya perjalanan ke segala arah melintasi area persegi yang dicakupnya. Grid raster ini biasanya dibuat dengan menerapkan model Indeks menggunakan aljabar Peta untuk menghitung total biaya dari raster terpisah yang mewakili elemen biaya individual. Dengan demikian "jarak" antara dua titik di sepanjang tambalan yang diberikan adalah akumulasi dari semua biaya yang relevan untuk setiap titik di jalan. Pada contoh jalur sepeda, jalur di atas bukit mungkin memiliki jarak biaya yang sama dengan jalur yang mengelilingi bukit, meskipun jalur sebelumnya adalah garis lurus pada peta.

Analysis Tools

Sebagian besar perangkat lunak GIS berisi sejumlah alat untuk melakukan berbagai tugas yang tergantung pada biaya dan jarak biaya ke dalam akun. Sebagian besar alat ini memerlukan satu untuk pertama kali Cost surface menggunakan alat GIS lain seperti Map algebra.

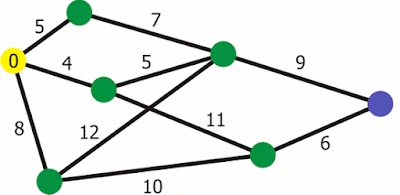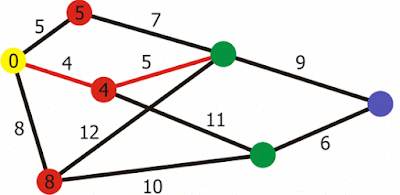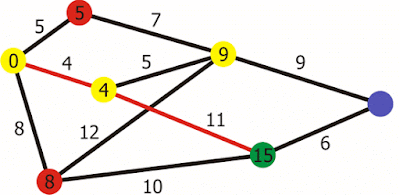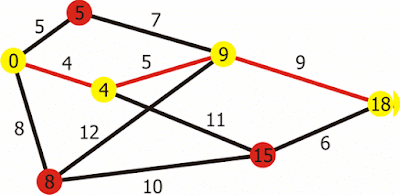
COST DISTANCE

The cost distance tool mirip dengan Euclidean distance raster tools,  tetapi alih-alih menghitung jarak aktual dari sel yang diberikan ke seluruh sel, alat jarak biaya menentukan jarak tertimbang paling pendek (atau akumulasi biaya perjalanan) dari setiap sel ke lokasi sumber terdekat. Alat-alat ini berlaku jarak dalam satuan biaya,  bukan dalam satuan geografis. Alat jarak biaya membutuhkan satu atau lebih lokasi sumber dan raster biaya sebagai input. Setiap sel dari grid jarak biaya yang dihasilkan berisi total biaya minimal untuk melakukan perjalanan dari lokasi sumber yang  diberikan ke sel itu. 

Secara bersamaan, alat ini menciptakan grid raster kedua yang dikenal sebagai raster backlink yang mengkodekan, untuk setiap sel, arah ke sel tetangga dengan biaya terendah (yaitu, di mana jalur berbiaya terendah akan datang dari untuk sampai ke sel ini). Biasanya nilainya adalah arah yang dikodekan, seperti angka antara 0-7.

Algoritma brute-force dasar untuk menghitung jarak biaya adalah sebagai berikut, 

pada dasarnya menyebar dari sumber untuk mengisi seluruh grid:

• Buat daftar sel untuk dievaluasi, awalnya terdiri dari sel yang sesuai dengan lokasi sumber yang diberikan. 
• Untuk setiap sel dalam daftar:

1. Jika itu adalah sel sumber, tetapkan biaya 0
2. Jika tidak, lihat 8 sel tetangganya dan identifikasi tetangganya dengan biaya terendah.
3. Tetapkan nilai sel dalam raster backlink dengan kode untuk tetangga berbiaya terendah
4. Tambahkan nilai untuk sel ini dalam raster biaya ke biaya tetangg (kalikan dengan 1,414 untuk diagonal diagonal).
5. Identifikasi tetangga yang memiliki nilai lebih tinggi dari sel ini atau tidak ada nilai sama sekali dan tambahkan mereka ke daftar.

Algoritma ini agak tidak efisien, di mana banyak sel akan ditambahkan ke daftar,dan dengan demikian dievaluasi berulang kali. Beberapa algoritma yang lebih efisien telah dikembangkan. 

Cost Path Analysis

Setelah jarak biaya dan raster backlink dibuat,  jalur dengan biaya terendah dapat dibuat antara sumber dan satu atau lebih tujuan, dengan melacak kode arah backlink kembali dari tujuan kembali ke sumber.

Cost-Based Allocation

Alokasi Biaya membuat kisi-kisi raster di mana setiap sel dikodekan dengan sumber mana (dengan asumsi banyak sumber disediakan untuk alat) dapat dicapai dengan biaya minimum. Dengan demikian, raster alokasi yang dihasilkan terdiri dari daerah di sekitar masing-masing sumber. Dengan demikian alat ini analog dengan diagram Voronoi untuk jarak euclidean, dan alat alokasi Lokasi untuk jaringan.

Corridor Analysis

Analisis Koridor mirip dengan Analisis Jalur Biaya, tetapi alih-alih mengidentifikasi rute optimal tunggal antara dua titik, analisis ini dapat mengidentifikasi semua rute yang berada di bawah ambang biaya tertentu. Ini biasanya mengambil bentuk petak luas wilayah antara sumber dan tujuan, sebagai lawan dari jalur sel satu. Pendekatan ini paling berguna untuk aplikasi di mana jalur tunggal tidak perlu dipilih, hanya area umum jalur yang dapat diterima, seperti dalam pemodelan migrasi satwa liar.

Cara untuk melakukan Cost Distance

Algoritma Ant Colony

Dasar algoritma ini adalah kemampuan dari sekumpulan semut (colony) yang mampu menemukan jalur terpendek dari sarangnya ke sumber makanan. Hal ini dapat dilakukan karena ketika semut berjalan pasti akan meninggalkan jejak berupa bau atau yang sering disebut pheromone. Berikut gambar dari tingkah laku semut pada umumnya.

Gambar Ant Colony System

Seiring perkembangan algoritma dari ant koloni ini, munculah algoritma pengembangan dari algoritma ant koloni antara lain: ant coloni optimization dan multiple ant coloni sistem.

 Ant colony optimization (ACO)

Algoritma Ant Colony Optimization (ACO) merupakan salah satu metode metaheuristik yang menerapkan semut sebagai agen dengan update Pheromone-nya untuk dapat melakukan proses pencarian solusi yang efektif dan efisien. Ant Colony Optimization (ACO) diadopsi dari perilaku koloni semut yang dikenal sebagai system semut (Dorigo, M., dan Gambardella, L., 1996). Pada ACO setiap semut ditempatkan di semua titik graph (dalam hal ini titik – titik yang dikunjungi) yang kemudian akan bergerak mengunjungi seluruh titik. Setiap semut akan membuat jalur masing – masing sampai kembali ketempat semula dimana mereka ditempatkan pertama kali. Jika sudah mencapai keadaan ini, maka semut telah menyelesaikan sebuah siklus (tour). Solusi akhir adalah jalur terpendek dari seluruh jalur yang dihasilkan oleh pencarian semut tersebut.

Algoritma ACO telah banyak diaplikasikan dalam berbagai bidang yang mencakup beberapa persoalan, yaitu :

1. Traveling Salesman Problem (TSP), yaitu mencari rute terpendek dalam sebuah graph menggunakan rute Hamilton.

2. Quadratic Assignment Problem (QAP), yaitu menugaskan sejumlah n resources untuk ditempatkan pada sejumlah m lokasi dengan meminimalisasi biaya penugasan (assignment).

3. Job-shop Scheduling Problem (JSP) juga salah satu contoh aplikasi Ant Colony Optimization, yaitu untuk mencari lintasan sejumlah n pekerjaan menggunakan sejumlah m mesin demikian sehingga seluruh pekerjaan diselesaikan dalam waktu yang seminimal mungkin.

4. Vehicle Routing Problem (VRP)

5. Pengaturan rute kendaraan

6. Pewarnaan graph

7. Implementasi pada jaringan komunikasi

8. Network routing, dll.

Algoritme A-star (A*)

Metode A-Star dikembangkan oleh Peter Hart, Nils Nilsson, dan Bertram Raphael. A* (disebut “A-star”) adalah sebuah graph atau metode pohon pencarian yang digunakan untuk mencari jalan dari sebuah node awal ke node tujuan yang telah ditentukan (Hart et al., 1968). Metode ini menggunakan “estimasi heuristic” dimana heuristik adalah penilai yang memberi harga pada tiap simpul yang memandu A* mendapatkan solusi yang diinginkan. Dengan heuristik yang benar, maka A* pasti akan mendapatkan solusi jika memang ada solusi yang dicari (Tilawah, 2010). Nilai Heuristik h(x) pada setiap node untuk mengurutkan setiap node x berdasarkan estimasi rute terbaik yang melalui node tersebut. Algoritme A* mencari jalur dengan cost terkecil dari node awal ke node berikutnya sampai mencapai node tujuan. Dalam penentuan rute terbaik, A* memiliki suatu fungsi yang dinotasikan dengan f(x) untuk menetapkan estimasi cost yang terkecil dari jalur yang dilalui node x. Adapun fungsi f(x) dapat dirumuskan sebagai berikut .(Irsyad dan Rasila, 2015).

f(x) = h(x) + g(x)

dimana,

f (x) : Biaya yang dibutuhkan

g(x) : Biaya yang ditempuh dari node asal

h(x) : Nilai perkiraan dari node saat ini hingga ke tujuan

Sebagai contoh berikut adalah sebuah diagram sederhana untuk menggambarkan

g(x):

Gambar 2.7 Contoh diagram (Hart et al., 1968)

        Pada gambar 2.7 dapat dilihat node awal adalah titik s, dan tiga titik lainya yaitu n1, n2 dan n3. Dimulai dari titk S menuju n1 dan n2. Dianggap nilai g(n1) dan g(n2) adalah 3 dan 7. Misalkan A* menghubungkan n1 dengan n3 dan n2, maka g(n3)=3+2=5 lebih rendah dibanding g(n2)=3+3=6. Fungsi h(x) adalah hyphotesis cost atau heuristic cost atau estimasi cost terkecil dari node x ke tujuan, yang disebut juga sebagai future pathcost. h(x) mewakili garis lurus jarak ke titik tujuan. Jarak diantara dua titik yang dapat dihitung dengan menggunakan Metode Harversine dan Metode Euclidean

Algoritma Dijkstra

Saat ini sudah banyak algoritma yang bisa digunakan untuk menemukan pencarian rute terpendek, dan tidak bisa di pungkiri Djikstra masih menjadi salah satu yang populer dari sekian banyak algoritma tersebut. Pada postingan kali ini kita akan membahas mendetail mulai dari apa itu algoritma djikstra dan dan bagaimana cara kerja algoritma djikstra.

Algortima ini ditemukan oleh Edsger W. Dikstra dan di publikasi pada tahun 1959 pada sebuah jurnal Numerische Mathematik yang berjudul “A Note on Two Problems in Connexion with Graphs“[1]. Algoritma ini sering digambarkan sebagai algoritma greedy (tamak). Sebagai contoh, ada pada buku Algorithmics(Brassard and Bratley [1988, pp. 87-92])

Djikstra merupakan salah satu varian bentuk algoritma popular dalam pemecahan persoalan terkait masalah optimasi pencarian  lintasan terpendek sebuah lintasan yang mempunyai panjang minimum dari verteks a ke z dalam graph berbobot, bobot tersebut adalah bilangan positif jadi tidak dapat dilalui oleh node negatif. Namun jika terjadi demikian, maka penyelesaian yang diberikan adalah infiniti (Tak Hingga). Pada algoritma Dijkstra, node digunakan karena algoritma Dijkstra menggunakan graph berarah untuk penentuan rute listasan terpendek. Berikut Flowchart Algoritma Djikstra:

Gambar Flowchart Dijkstra

Implementasi Djikstra

Algoritma ini bertujuan untuk menemukan jalur terpendek berdasarkan bobot terkecil dari satu titik ke titk lainnya. Misalnya titik mengambarkan gedung dan garis menggambarkan jalan, maka algoritma Dijkstra melakukan kalkulasi terhadap semua kemungkinan bobot terkecil dari setiap titik.

Pertama-tama tentukan titik mana yang akan menjadikan node awal, lalu beri bobot jarak pada node pertama ke node terdekat satu persatu, Dijkstra akan melakukan pengembangan pencarian dari satu titik ke titik lain dan ke titik selanjutnya tahap demi tahap inilah urutan logika dari algoritma Dijkstra :

1.      Beri nilai bobot (jarak) untuk setiap titik ke titik lainnya, lalu set nilai 0 pada node awal dan nilai tak hingga terhadap node lain (belum terisi)

2.      Set semua node “Belum Terjamah” dan set node awal sebagai “Node keberangkatan”

3.      Dari no keberangkatan, pertimbangkan node tetangga yang belum terjamah dan hitung jaraknya dari titik keberangkatan. Sebagai contoh, jika titik keberangkatan A ke B memiliki bobot jarak 6 dan dari B ke node C berjarak 2, maka jarak ke C melewati B menjadi 6+2=8. Jika jarak ini lebih kecil dari jarak sebelumnya (yang telah terekam sebelumnya) hapus data lama, simpan ulang data jarak dengan jarak yang baru.

4.      Saat kita selesai mempertimbangkan setiap jarak terhadap node tetangga, tandai node yang telah terjamah sebagai “Node terjamah”. Node terjamah tidak akan pernah di cek kembali, jarak yang disimpan adalah jarak terakhir dan yang paling minimal bobotnya.
5.  Set “Node belum terjamah” dengan jarak terkecil (dari node keberangkatan) sebagai “Node Keberangkatan” selajutnya dan lanjutkan dengan kembali ke step 3